PCA(Principal Components Analysis)
主成分分析作為降維最經典的方法,它屬於一種線性、非監督、全域的降維演算法。PCA的目的是找到資料中的主成份,並利用他們表徵原始資料,進而達到降為的目的
將n維特徵映射到k維上,這k維是全新的正交特徵也被稱為主成份,是在原有n維特徵基礎上重新構造出來的k維特徵。
首先先假設一組數據包含n個m維樣本

現在將樣本降至k維,使用一個矩陣V變換得到y


這樣降維問題就就變成如何得到這個V了
首先先討論兩個東西
1. 向量內積

由於可以將v進行縮放,所以約束使其為1,及|v|=1,於是得到

可以發現v與樣本內積就是樣本在v上面的投影長度
2.散度

在PCA中,我們需要找到一個超平面來滿足最大可分性,亦即樣本點在這個平面上的投影能盡可能的分開,而這個分開程度我們稱為散度,這邊我們採用樣本協方差來衡量這個散度。以上圖的黃線來看,此軸的資料分布的更散意味著樣本點在這個方向的變異數更大
在信號處理領域中,一般認為信號具有較大的變異數,雜訊則具有較小的變異數,信號與雜訊之比稱為信噪比,信噪比越大代表資料的品質越好。
在我們進行PCA之前,我們會先將資料中心化,而中心化後平均為0


樣本協方差矩陣

樣本在V上投影的方差

故我們的目標即是找到一個V來最大化散度(方差)
再加上前面提到的約束條件|V|=1

這是一個常見的優化問題,透過拉格朗日乘數可以建構出一個目標式

對V進行偏微分

令上式等於0,可以得到
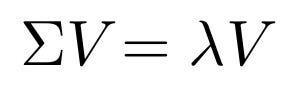
由上式可以觀察到λ其實就是Σ特徵值,V是對應的特徵向量,我們只要將所有的特徵值排序然後選擇前k個最大的特徵值對應的向量
將即帶回至投影協方差中

由此推出投影後的方差就是樣本協方差矩陣Σ的特徵值
以下列出PCA求解步驟:
- 對樣本進行中心化處理
- 求出樣本協方差矩陣(共變異數矩陣)
- 對樣本協方差矩陣(共變異數矩陣)進行特徵值分解,並將特徵值從小到大排列
- 取特徵值前k大對應的特徵向量v1, v2, …, vk

透過選取前k大的特徵值對應的特徵向量,首先拋棄變異較小的特徵(雜訊),使的每個n為列向量xi映射為k維列向量yi
這邊有一個公式可以衡量降維後的資訊佔比:

最後附上Python code
